Prépa MPSI · Lycée Saint-Rémi · 2025

Simulation proies-prédateurs

Reproduire 60 ans de dynamique écologique avec des règles simples

PythonNumPyMatplotlibModélisation

Découvrir le projet ↓ Code source

Animation de la simulation proies-prédateurs sur grille 50×50

Orignaux Loups Vide

2 500 cellules simulées

70+ générations par simulation

60 ans de données réelles (Isle Royale)

4 phases comportementales

01 — Le problème

Peut-on reproduire la nature
avec des règles simples ?

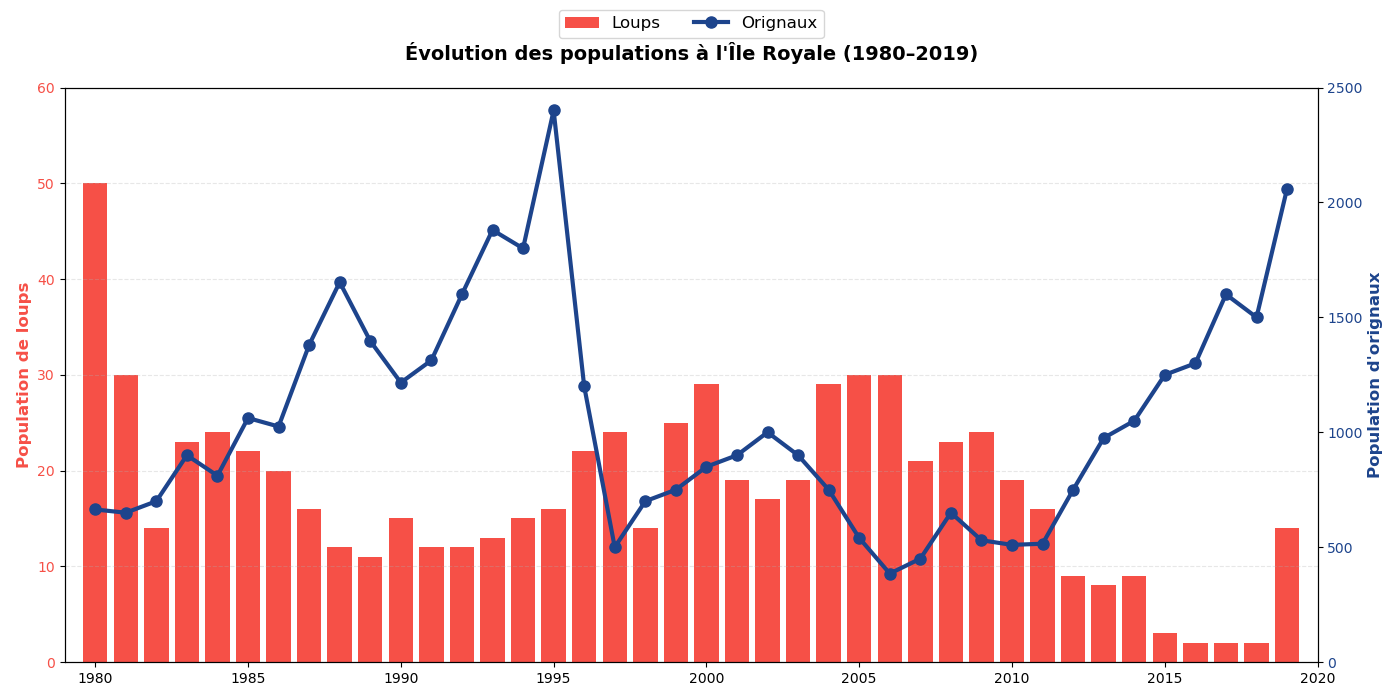
Depuis 1958, les scientifiques observent un phénomène fascinant sur l'Isle Royale (Michigan) : les populations de loups et d'orignaux oscillent dans un cycle perpétuel. Quand les proies abondent, les prédateurs prospèrent… puis déciment les proies, entraînant leur propre déclin.

Cet écosystème isolé offre des conditions idéales pour étudier ces dynamiques. Ma question : peut-on les reproduire informatiquement à partir de règles locales simples, inspirées du jeu de la vie de Conway ?

« Dans quelle mesure peut-on reproduire les cycles d'évolution d'un système proies-prédateurs à l'aide d'une simulation informatique ? »

Évolution des populations à l'Île Royale (1980-2019) — Données réelles — Isle Royale (1980–2019). Les barres rouges représentent les loups, la courbe bleue les orignaux.

02 — Le parti pris

Traduire le réel, pas les équations

🚫

Pas de Lotka-Volterra

Le modèle classique proies-prédateurs existe depuis 1926. Je l'ai volontairement écarté pour tester une autre hypothèse : est-ce que la simple traduction des comportements observés dans la réalité suffit à produire des dynamiques cohérentes ? Pas d'équations différentielles. Juste de la logique locale tirée de l'observation.

🔧

Des outils fondamentaux

Le code repose volontairement sur des structures basiques de Python : boucles, matrices sous forme de listes, conditions. Pas de framework de simulation, pas de librairie spécialisée. Chaque mécanisme est codé à la main pour maîtriser chaque rouage du système, et rester dans le cadre de la prépa.

🎯

Mon propre jeu de la vie

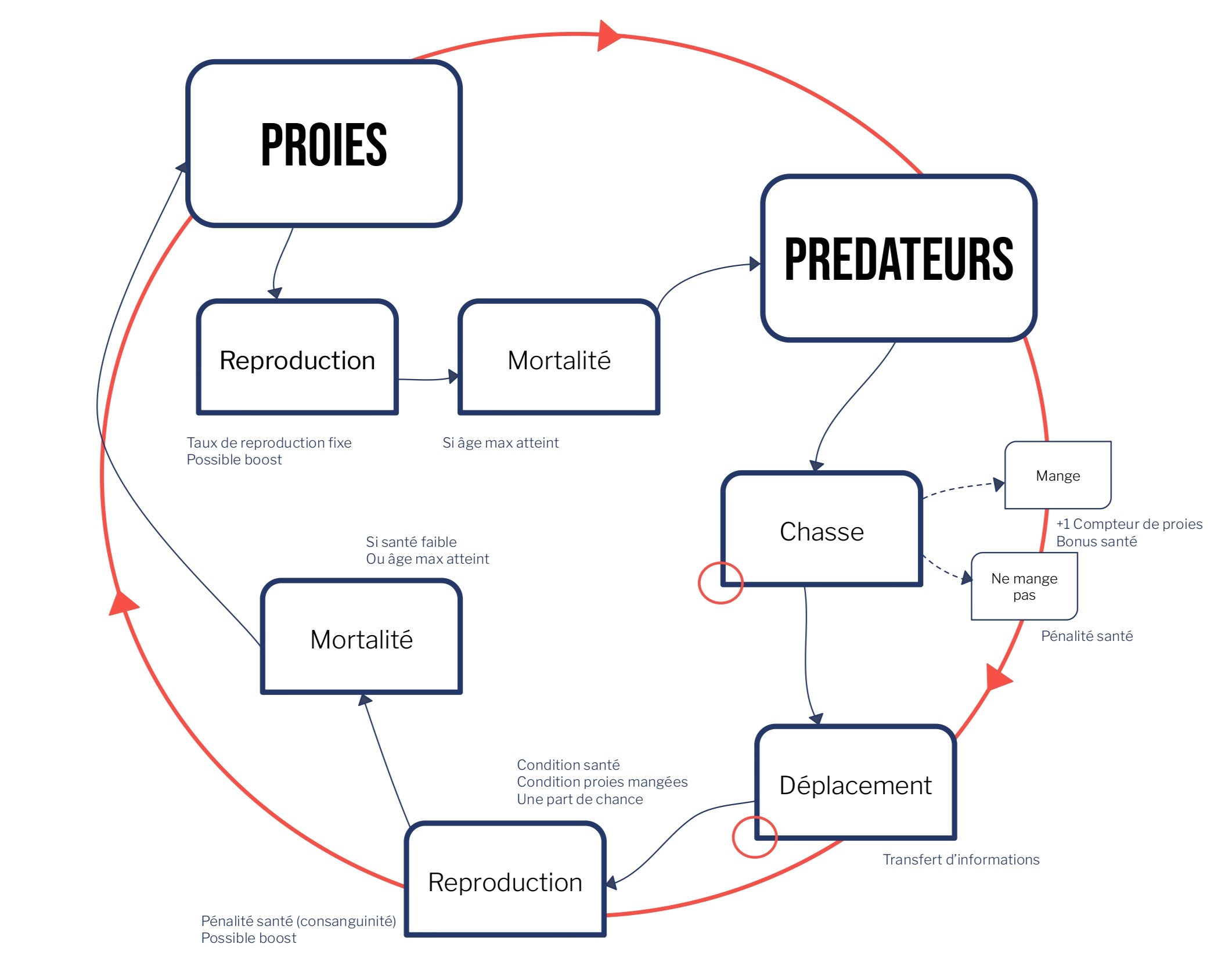
L'objectif n'était pas de reproduire le Game of Life de Conway, mais de créer mes propres règles en partant d'une analyse concrète : pourquoi un loup chasse, comment il se déplace, quand il meurt. Chaque règle traduit un comportement réel, pas une abstraction mathématique.

03 — L'approche

Un modèle inspiré du jeu de la vie

Chaque cellule d'une grille 50×50 peut être vide, contenir une proie ou un prédateur. À chaque génération, des règles locales déterminent l'évolution du système. Exemple : comportement des loups ↓

🎯

Chasse

Le prédateur scanne ses voisins. S'il trouve une proie, il la mange et gagne en santé.

→

🔄

Déplacement

S'il ne mange pas, le loup se déplace vers une case vide et subit une pénalité santé.

→

🐺

Reproduction

Si assez de proies mangées, santé suffisante et un peu de chance → nouveau loup.

→

💀

Mortalité

Âge maximal atteint ou santé trop faible → le prédateur meurt.

Mécanismes adaptatifs

Survie

Seuil critique

Quand les loups tombent sous 25 individus, un bonus de santé et un seuil de reproduction réduit s'activent pour éviter l'extinction.

Génétique

Consanguinité

Les nouveaux loups naissent avec une santé réduite, simulant les effets de la consanguinité observés sur l'Isle Royale.

Équilibre

Boost proies

Si les prédateurs sont rares, les orignaux bénéficient d'un taux de reproduction augmenté, ce qui relance le cycle naturel.

Schéma du cycle proies-prédateurs — boucle update complète — Vue d'ensemble : le cycle complet des interactions proies ↔ prédateurs avec les conditions de chaque phase.

04 — Les résultats

La simulation reproduit les cycles réels

Données réelles Isle Royale — Isle Royale, 1980–2019

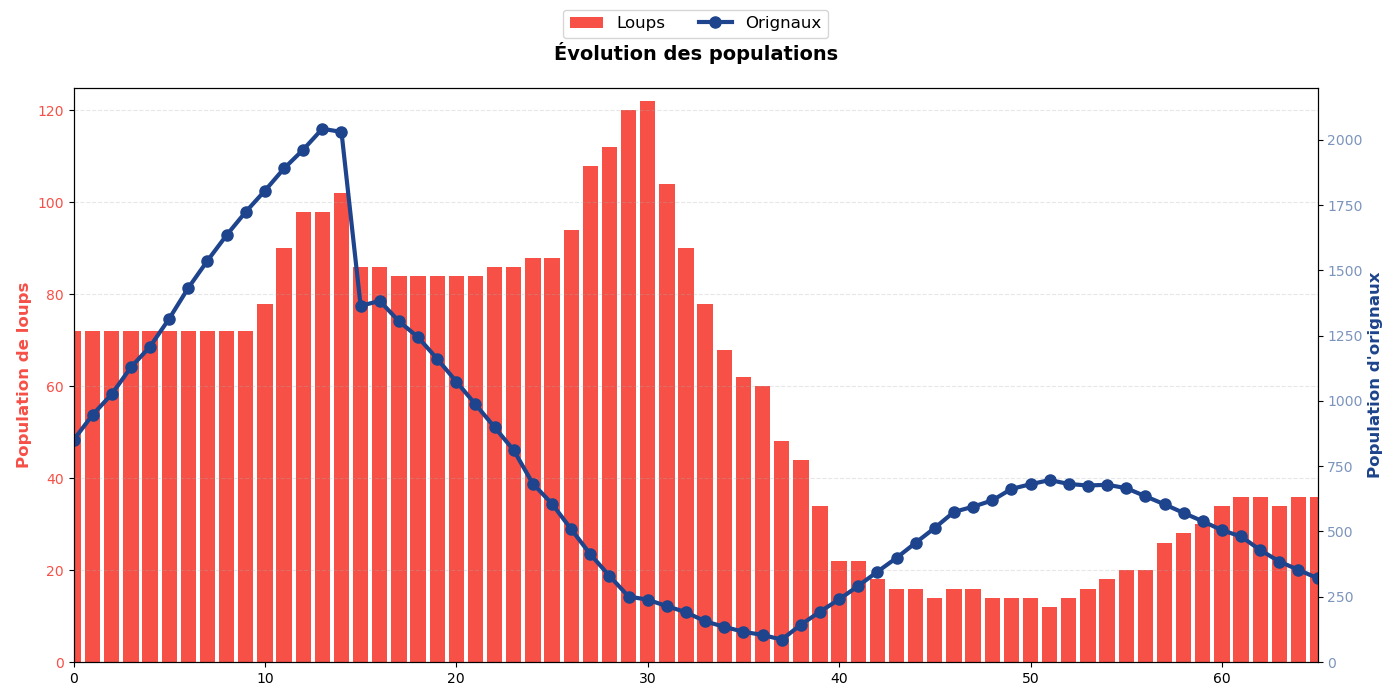
Graphe de la simulation — Grille 50×50, 70 générations

✓

Décalage de phase reproduit

L'augmentation des prédateurs suit celle des proies avec un retard temporel, exactement comme dans les données réelles.

✓

Oscillations cohérentes

Les fluctuations non périodiques du modèle probabiliste reflètent la variabilité naturelle de l'écosystème.

✓

Émergence comportementale

Des règles locales simples suffisent à produire un comportement global cohérent avec 60 ans de données réelles.

05 — Évolution visuelle

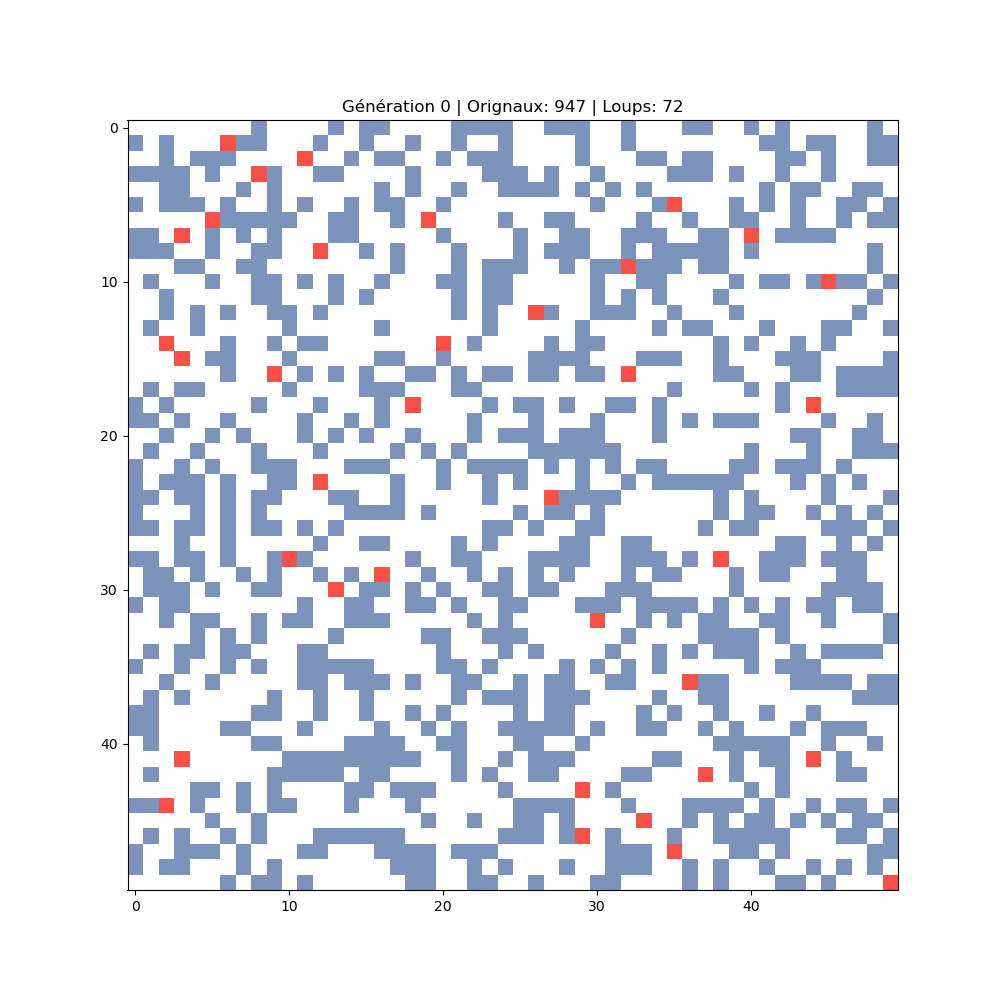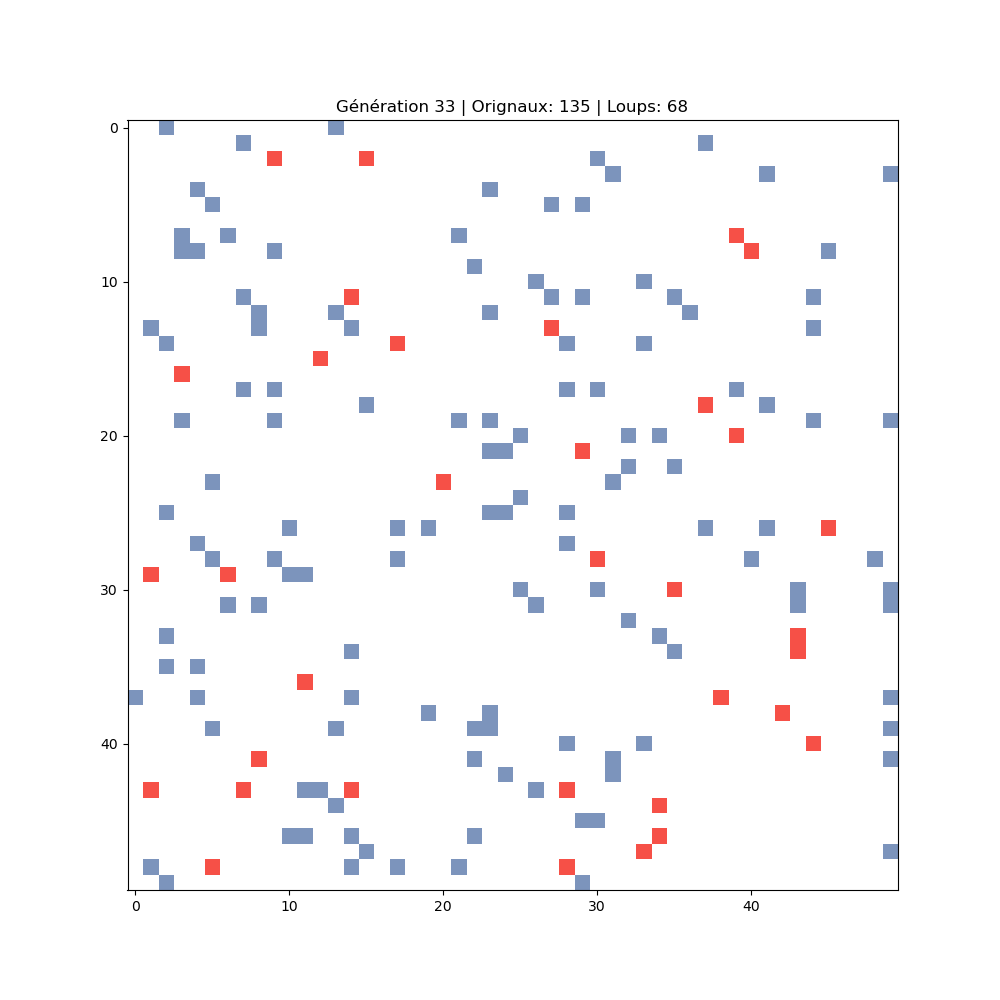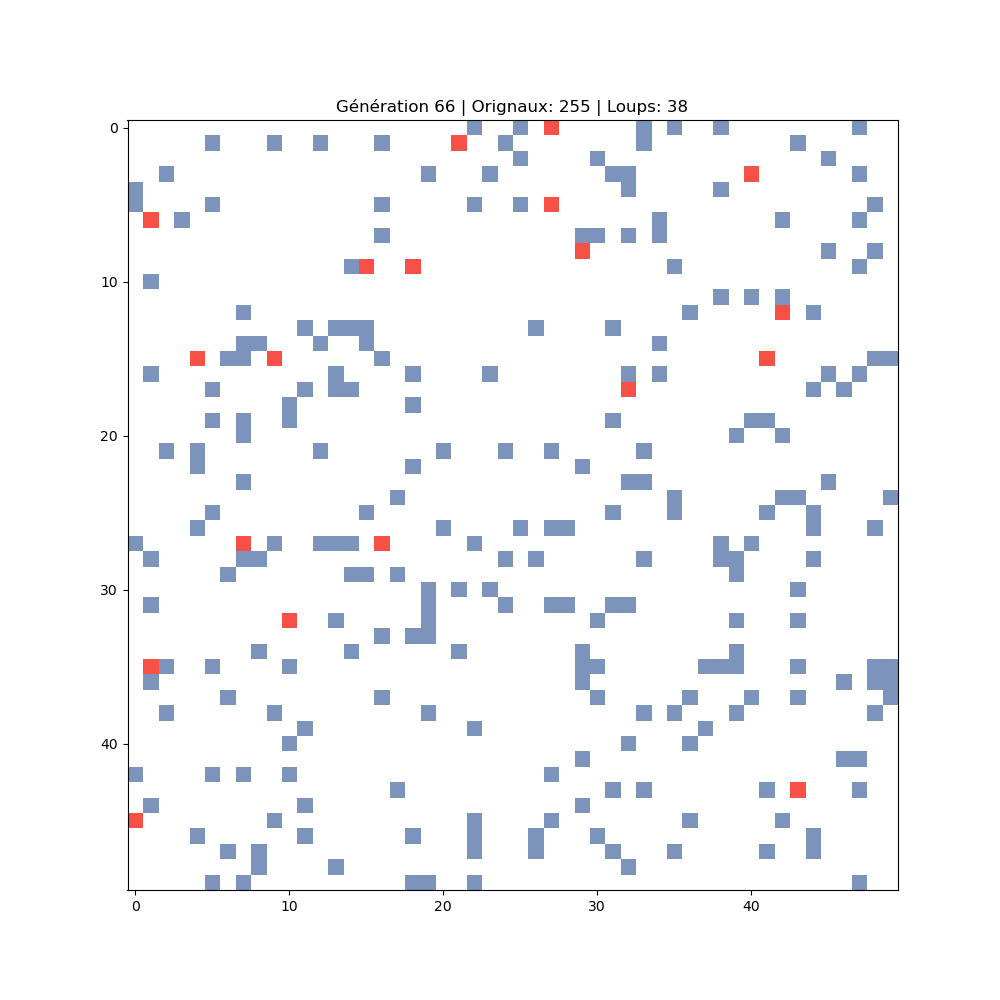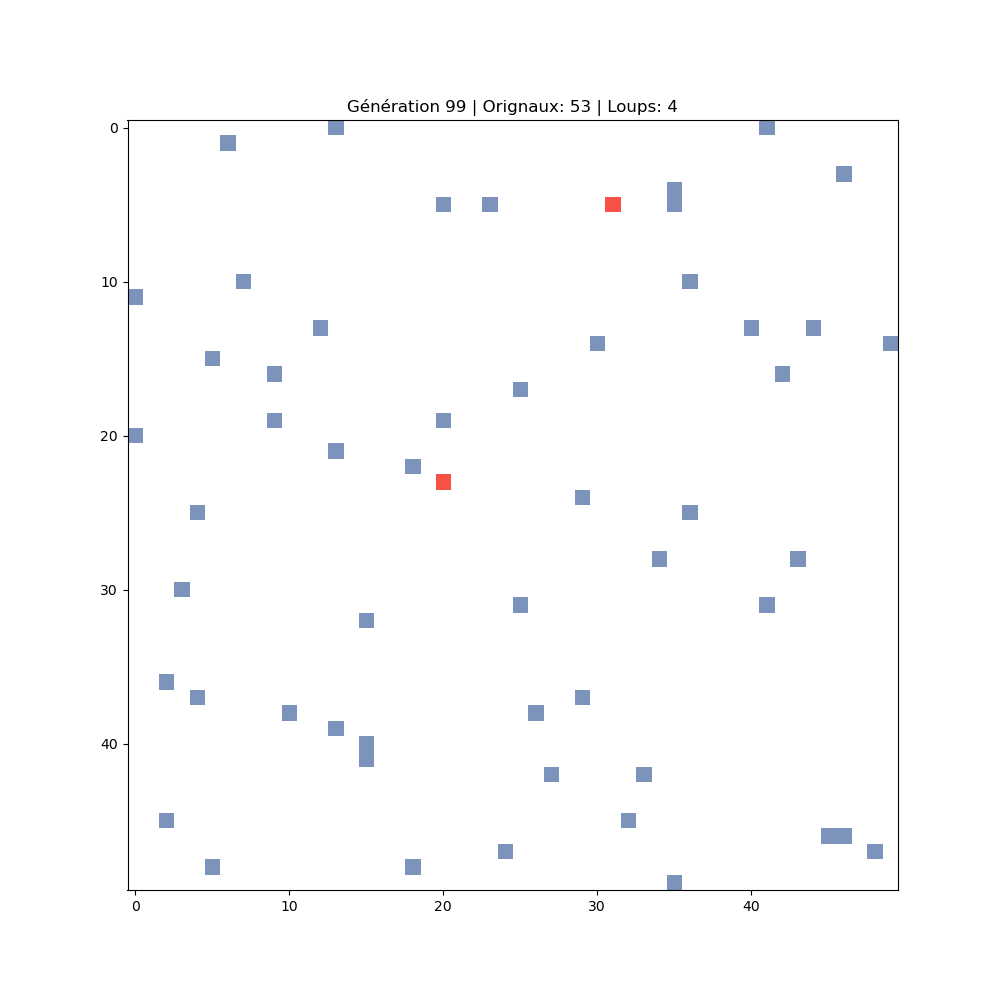
La grille à travers les générations

Chaque image montre un instant de la simulation. On observe l'expansion des proies, suivie de l'explosion des prédateurs, puis l'effondrement et la reprise du cycle.

Gén. 12

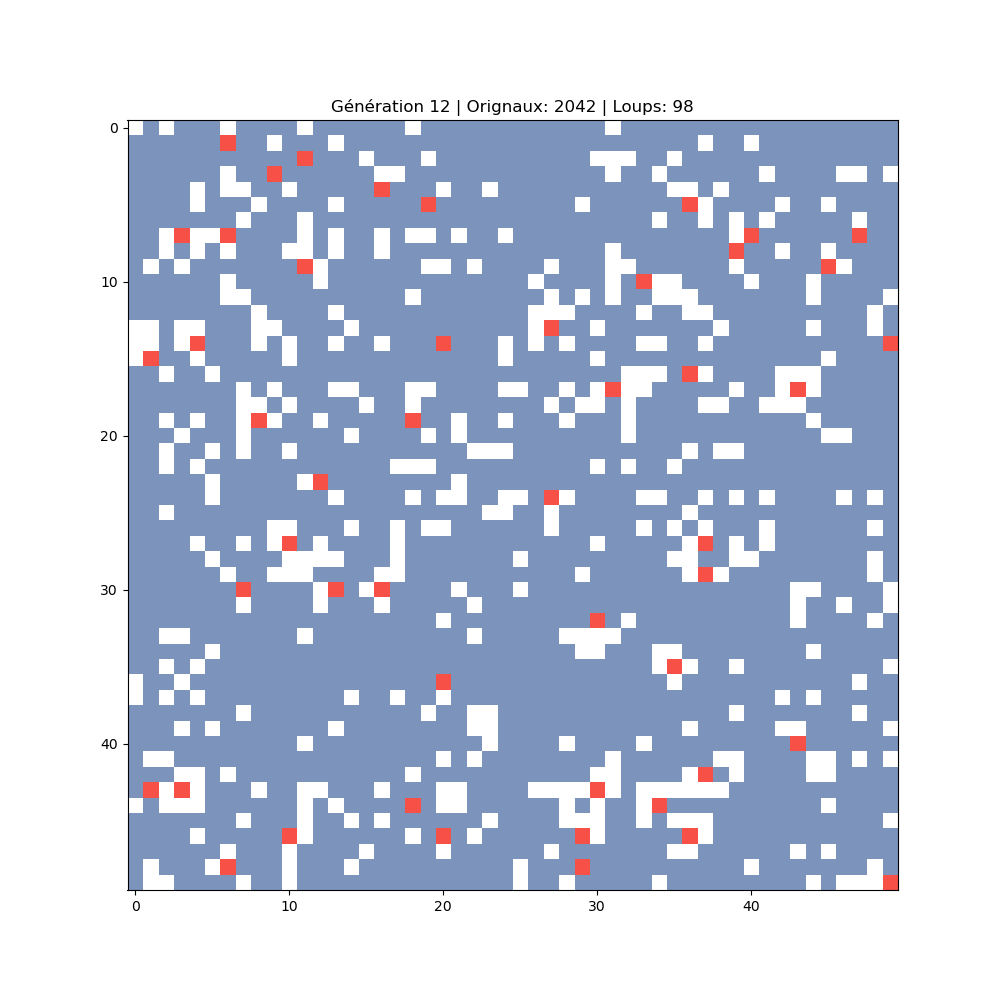
2 042 orignaux · 98 loups
Expansion maximale des proies

Gén. 29

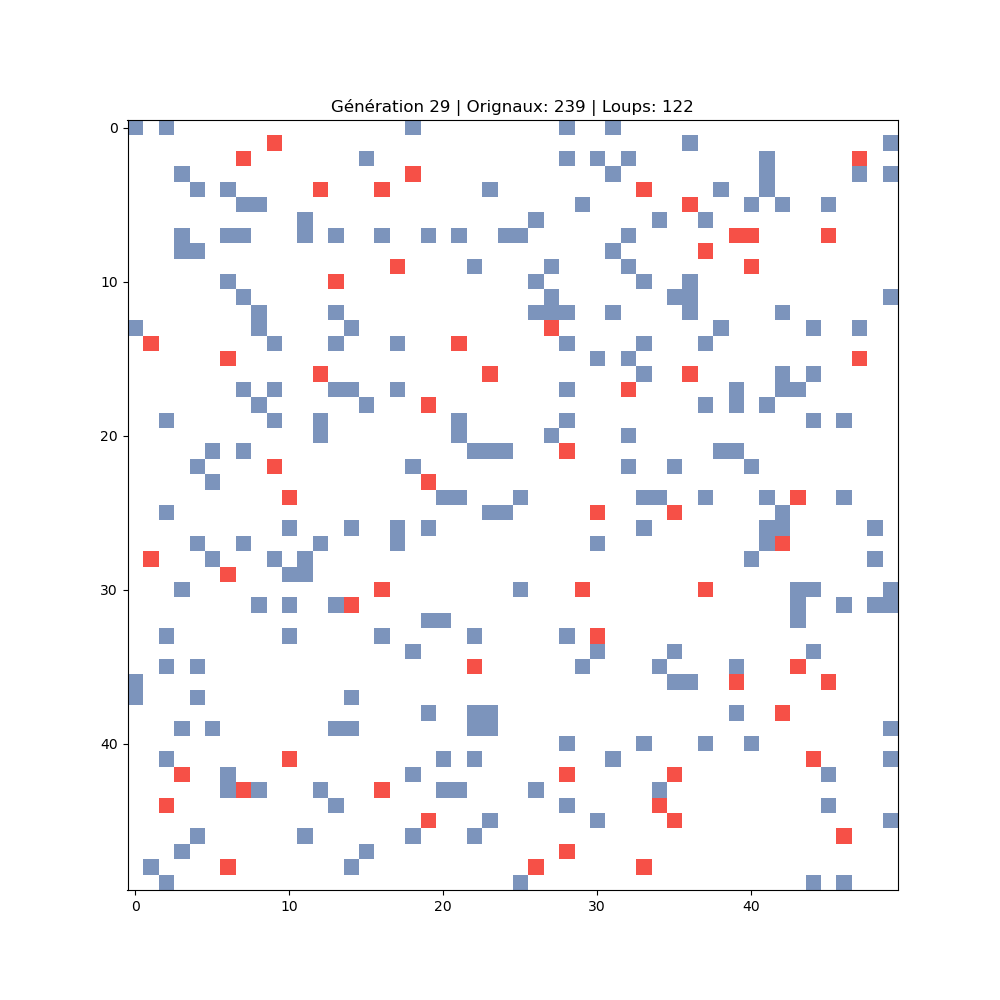
239 orignaux · 122 loups
Pic prédateurs, effondrement proies

Gén. 50

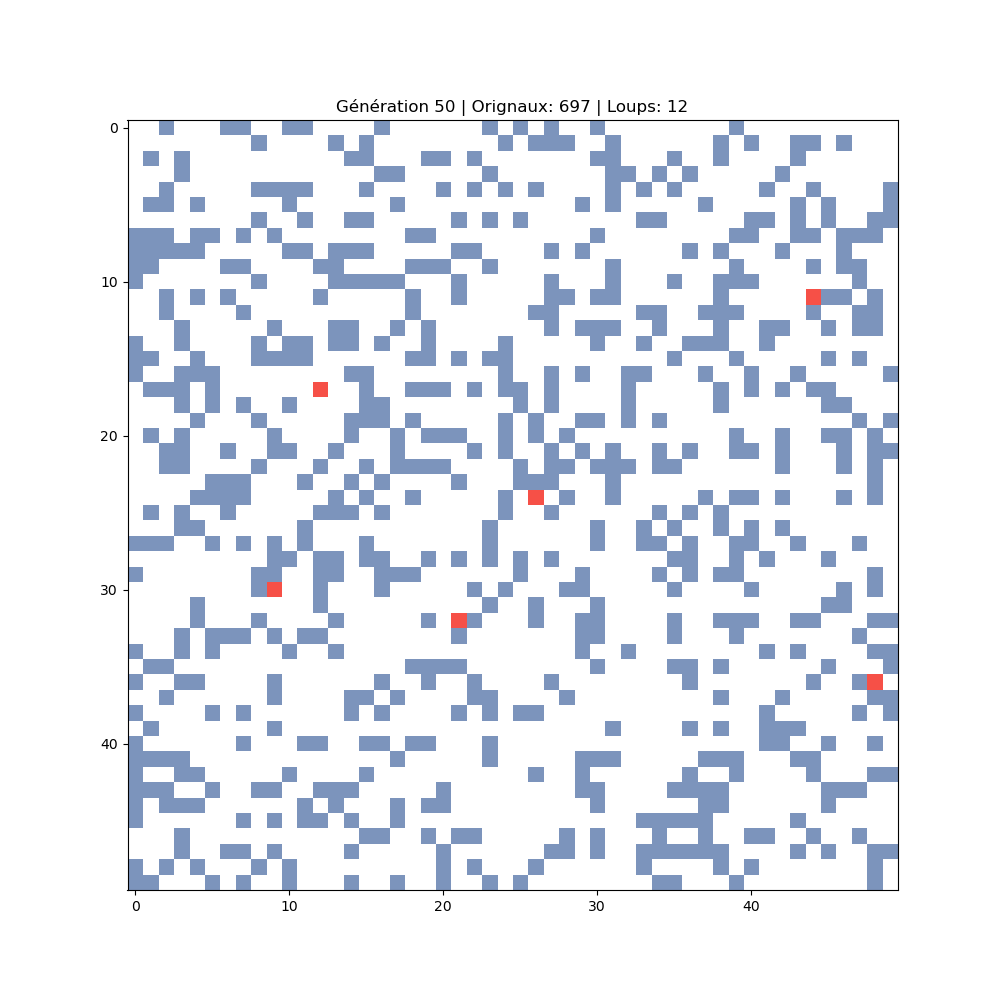
697 orignaux · 12 loups
Déclin des loups, reprise du cycle

Gén. 67

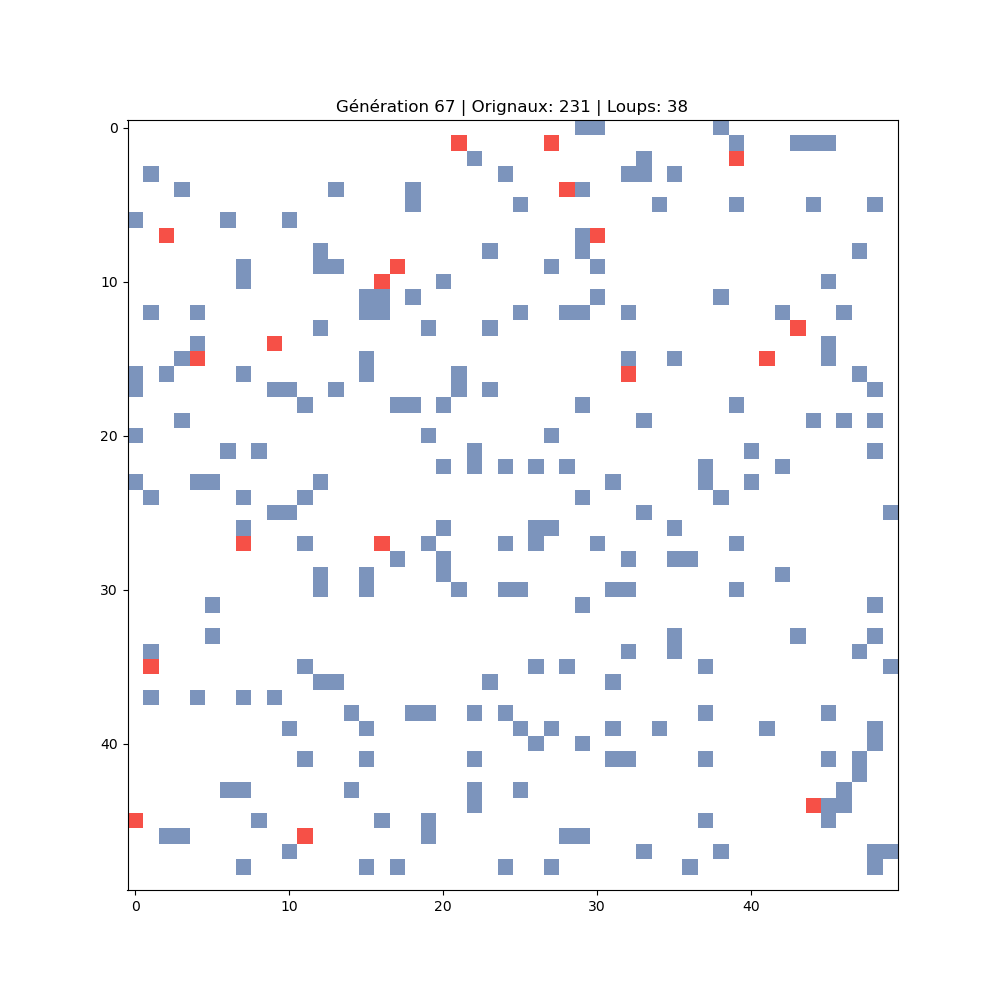
231 orignaux · 38 loups
Nouveau cycle en cours

06 — Limites & recul

Ce que le modèle ne capture pas

Un bon modèle est aussi défini par ce qu'il reconnaît ne pas couvrir. Sur le long terme ou avec des paramètres extrêmes, le système diverge.

Simplifications

Pas de saisons ni de variation climatique
Pas de migration, l'île est fermée
Génétique et maladies peu détaillées
Paramètres de simulation fixes

Cas d'effondrement

Sur 500 générations, les loups finissent par s'éteindre (génération 396 : 22 orignaux, 0 loup). Sur une grille de 100×100, ce sont les orignaux qui disparaissent en premier. Le modèle ne maintient pas l'équilibre indéfiniment.

Pistes d'amélioration

Introduction de facteurs environnementaux
Reproduction spatialement localisée
Répétition de simulations pour moyennage statistique
Paramètres adaptatifs au fil des générations

07 — Et ensuite ?

Vers une simulation qui s'améliore d'elle-même

Le modèle actuel repose sur des paramètres fixés à la main : taux de reproduction, seuils de santé, pénalités. Ces choix fonctionnent, mais ils sont le fruit de mon intuition et de mes essais, pas d'une optimisation rigoureuse.

Je travaille actuellement sur l'intégration d'un algorithme génétique pour calibrer automatiquement ces paramètres. Le principe : générer des centaines de simulations avec des configurations différentes, évaluer leur proximité avec les données réelles de l'Isle Royale, et faire "survivre" les meilleures configurations, génération après génération.

🧬

L'idée : appliquer la logique de la sélection naturelle non plus aux loups et aux orignaux, mais aux paramètres de la simulation elle-même. Faire évoluer le modèle pour qu'il apprenne à reproduire le réel.

C'est une transition naturelle vers le machine learning : passer d'un modèle conçu manuellement à un modèle qui s'optimise par les données. Et c'est exactement la direction de ma spécialisation en Data & IA.

Ce que ce projet m'a appris

Ce travail montre qu’il est possible de reproduire partiellement les dynamiques d’un système réel à l’aide d’un modèle numérique simple. La simulation ne cherche pas à remplacer la complexité du vivant, mais à comprendre les mécanismes fondamentaux qui gouvernent l’évolution d’un système complexe.

Ce projet illustre l’intérêt de la modélisation numérique comme outil d’ingénierie des systèmes, permettant d’analyser, tester et interpréter des comportements globaux à partir de règles locales, avant toute implémentation sur un système réel.